Hello!
Being new to GAMS I´m struggling with implementation of a simple two stage model, especially the EMP annotation part.
The model is described in the picture:
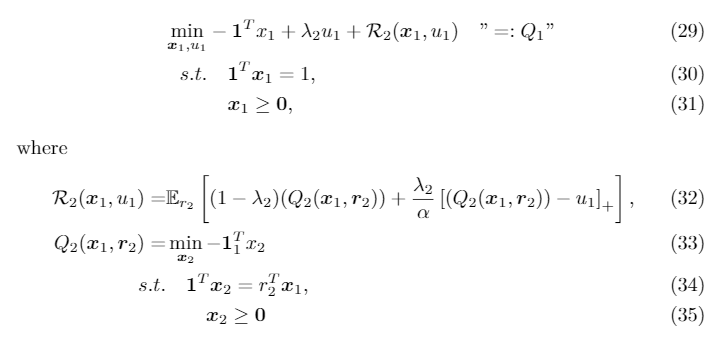
Variable r-2 - stock returns - is random and I want to approximate it by scenarios. lambda_2 and alpha are constants.
I started with the following code, but I can´t get the EMP part right probably:
$title Two stage asset allocation model
Sets n "assets" / att, gmc, usx /
j "scenarios" / s1*s4 / ;
Table r_scenarios(j,n) "scenario returns from assets"
att gmc usx
s1 1.300 1.225 1.149
s2 1.103 1.290 1.260
s3 1.216 1.216 1.419
s4 0.954 0.728 0.922 ;
Parameters
r(n) "return from assets"
p(j) "probability" / #j [1/card(j)] / ;
Scalars lambda_2 "mean-risk ratio" / 0.5 /
alpha "CVaR level" / 0.05/ ;
Variables
Q_1 "objective"
x_1(n) "first stage weights"
x_2(n) "second stage weights"
u_1 "first stage CVaR minimizer"
R_2 "recoursive part"
Q_2 "second stage objective" ;
Positive Variables x_1, x_2;
Equations
Q_1_equation "objective function"
budget_first "budget constraint for x_1"
R_2_equation "R_2 equation"
Q_2_equation "second stage objective function"
budget_second "budget constraint for x_2"
take_max "max(Q_2 - u_1, 0)";
Q_1_equation.. Q_1 =e= - sum(n, x_1(n)) + lambda_2 * u_1 + R_2;
budget_first.. sum(n, x_1(n)) =e= 1;
R_2_equation.. R_2 =e= (1-lambda_2)* Q_2 + (lambda_2 / alpha) * (Q_2 - u_1)
Q_2_equation.. Q_2 =e= - sum(n, x_2(n))
budget_second.. sum(n, x_2(n)) =e= sum(n, x_1(n)*r(n))
take_max.. Q_2 - u_1 =g= 0
Model portfolio / all /;
* EMP Annotations
File emp / '%emp.info%' /;
emp.nd=4;
put emp '* problem %gams.i%'
/ 'stage 2 ?????'
/ "jrandvar r('att') r('gmc') r('usx')"
loop(j,
put / p(j) r_scenarios(j,"att") r_scenarios(j,"gmc") r_scenarios(j,"usx"));
putclose emp;
Is my overall approach right and could you please help me to continue? The next step for me is to extend the model for multiple stages, but I guess it won´t be much different.
Thank you!
Here is a syntactically correct EMP model, but the feasible region is empty and the DE solver returns infeasible. Good luck debugging the model. -Michael
$title Two stage asset allocation model
Sets n "assets" / att, gmc, usx /
j "scenarios" / s1*s4 / ;
Table r_scenarios(j,n) "scenario returns from assets"
att gmc usx
s1 1.300 1.225 1.149
s2 1.103 1.290 1.260
s3 1.216 1.216 1.419
s4 0.954 0.728 0.922 ;
Parameters
r(n) "return from assets"
p(j) "probability" / #j [1/card(j)] / ;
Scalars lambda_2 "mean-risk ratio" / 0.5 /
alpha "CVaR level" / 0.05/ ;
Variables
Q_1 "objective"
x_1(n) "first stage weights"
x_2(n) "second stage weights"
u_1 "first stage CVaR minimizer"
R_2 "recoursive part"
Q_2 "second stage objective" ;
Positive Variables x_1, x_2;
Equations
Q_1_equation "objective function"
budget_first "budget constraint for x_1"
R_2_equation "R_2 equation"
Q_2_equation "second stage objective function"
budget_second "budget constraint for x_2"
take_max "max(Q_2 - u_1, 0)";
Q_1_equation.. Q_1 =e= - sum(n, x_1(n)) + lambda_2 * u_1 + R_2;
budget_first.. sum(n, x_1(n)) =e= 1;
R_2_equation.. R_2 =e= (1-lambda_2)* Q_2 + (lambda_2 / alpha) * (Q_2 - u_1);
Q_2_equation.. Q_2 =e= - sum(n, x_2(n));
budget_second.. sum(n, x_2(n)) =e= sum(n, x_1(n)*r(n));
take_max.. Q_2 - u_1 =g= 0
Model portfolio / all /;
* EMP Annotations
file emp / '%emp.info%' /; emp.nd=4;
put emp '* problem %gams.i%'
/ 'stage 2 r x_2 R_2 Q_2_equation budget_second take_max R_2_equation'
/ "jrandvar r('att') r('gmc') r('usx')"
loop(j,
put / p(j) r_scenarios(j,"att") r_scenarios(j,"gmc") r_scenarios(j,"usx"));
putclose emp;
r(n) = sum(j,r_scenarios(j,n))/card(j);
Parameter
srep(j,*) scenario attributes / #j.prob 0 /
j_r(j,n)
s_x_2(j,n);
Set dict / j .scenario.''
'' .opt. srep
r .randvar. j_r
x_2 .level. s_x_2 /;
solve portfolio min Q_1 us emp scenario dict;
Thank you very much! You helped me a lot.
Here is slightly changed verison which should work.
$title Two stage asset allocation model
Sets n "assets" / att, gmc, usx /
s "scenarios" / s1*s12 / ;
Table r_scenarios(s,n) "scenario returns from assets"
att gmc usx
s1 1.300 1.225 1.149
s2 1.103 1.290 1.260
s3 1.216 1.216 1.419
s4 0.954 0.728 0.922
s5 0.929 1.144 1.169
s6 1.056 1.107 0.965
s7 1.038 1.321 1.133
s8 1.089 1.305 1.732
s9 1.090 1.195 1.021
s10 1.083 1.390 1.131
s11 1.035 0.928 1.006
s12 1.176 1.715 1.908;
Parameters
r(n) "return from assets"
p(s) "probability" / #s [1/card(s)] / ;
Scalars lambda_2 "mean-risk ratio" / 0.5 /
alpha "CVaR level" / 0.05/ ;
Variables
Q_1 "objective"
x_1(n) "first stage weights"
x_2(n) "second stage weights"
u_1 "first stage CVaR minimizer"
R_2 "recoursive part"
Q_2 "second stage objective"
non_neg_part "non-negative part of Q_2 - u_1";
Positive Variables x_1, x_2, non_neg_part;
Equations
Q_1_equation "objective function"
budget_first "budget constraint for x_1"
R_2_equation "R_2 equation"
Q_2_equation "second stage objective function"
budget_second "budget constraint for x_2"
nnp_greater_than_Q_u " non_neg_part >= Q_2 - u_1";
Q_1_equation.. Q_1 =e= - sum(n, x_1(n)) + lambda_2 * u_1 + R_2;
budget_first.. sum(n, x_1(n)) =e= 1;
R_2_equation.. R_2 =e= (1-lambda_2)* Q_2 + (lambda_2 / alpha) * non_neg_part;
Q_2_equation.. Q_2 =e= - sum(n, x_2(n));
budget_second.. sum(n, x_2(n)) =e= sum(n, x_1(n)*r(n));
nnp_greater_than_Q_u.. non_neg_part =g= Q_2 - u_1;
Model portfolio / all /;
* EMP Annotations
file emp / '%emp.info%' /; emp.nd=4;
put emp '* problem %gams.i%'
/ 'stage 2 r x_2 Q_2 R_2 non_neg_part R_2_equation Q_2_equation budget_second nnp_greater_than_Q_u'
/ "jrandvar r('att') r('gmc') r('usx')"
loop(s,
put / p(s) r_scenarios(s,"att") r_scenarios(s,"gmc") r_scenarios(s,"usx"));
putclose emp;
r(n) = sum(s,r_scenarios(s,n))/card(s);
Parameter
srep(s,*) scenario attributes / #s.prob 0 /
s_r(s,n)
s_x_2(s,n);
Set dict / s .scenario.''
'' .opt. srep
r .randvar. s_r
x_2 .level. s_x_2 /;
solve portfolio min Q_1 us emp scenario dict;
display srep, s_r, s_x_2, x_1.l;
One thing is not completely right - s_x-2 is displayed only for “usx”. The same for x_1.l. How can I display the rest?
Perhaps, the optimization only selects usx for your portfolio. GAMS does not display zeros. You can force some other stocks with some constraints. -Michael