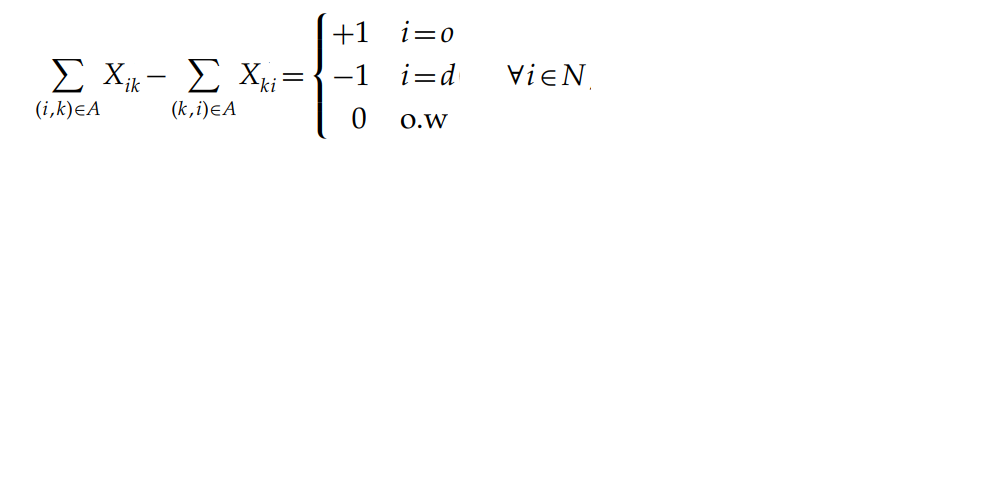I’m trying to solve the network problem below in GAMS Cplex. I have a piecewise constraint that are depending on the node situations (whether a node is an origin (o) node, inbetween node, and destination (d) node).
How do I write these piecewise contraints?
In the program below, I’ve write:
eq1 represents node 1 as an origin node,
eq2 eq3 eq4 represents node 2,3, and 4 as inbetween nodes,
eq5 represents node 5 as a destination node.
Set
i nodes /1,2,3,4,5/;
Alias(i,j);
Set
arc(i,j) arcs from node i to j
/1 .2
2 .1
1 .3
3 .1
1 .4
4 .1
2 .3
3 .2
2 .5
5 .2
3 .5
5 .3
4 .5
5 .4/;
Table c(i,j) population exposed from node i to node j
1 2 3 4 5
1 0 105000 90000 65000 0
2 105000 0 100000 0 85000
3 90000 100000 0 0 80000
4 65000 0 0 0 55000
5 0 85000 80000 55000 0
;
Table l(i,j) distance from node i to node j
1 2 3 4 5
1 0 5 8 10 0
2 5 0 2 0 7
3 8 2 0 0 11
4 10 0 0 0 8
5 0 7 11 8 0
Binary Variables
x(i,j)
y(i,j);
Positive Variables
v(i,j)
lambda(i,j);
Free Variables
w(i) node i
w(j) node j
z optimization solution;
Scalar
R very large number;
R = 10000000000000000;
Equations
sol optimization solution
eq1(i,j) constraint 1
eq2(i,j) constraint 2
eq3(i,j) constraint 3
eq4(i,j) constraint 4
eq5(i,j) constraint 5
eq6(i,j) constraint 6
eq7(i,j) constraint 7
eq8(i,j) constraint 8
eq9(i,j) constraint 9;
sol.. z =e= sum(arc(i,j),c(arc)*x(arc));
eq1(i,j).. x(1,2) - x(2,1) + x(1,3) - x(3,1) + x(1,4) - x(4,1) =e= 1;
eq2(i,j).. - x(1,2) + x(2,1) + x(2,3) - x(3,2) + x(2,5) - x(5,2) =e= 0;
eq3(i,j).. - x(1,3) + x(3,1) - x(2,3) + x(3,2) + x(3,5) - x(5,3) =e= 0;
eq4(i,j).. - x(1,4) + x(4,1) + x(4,5) - x(5,4) =e= 0;
eq5(i,j).. - x(2,5) + x(5,2) - x(3,5) + x(5,3) - x(4,5) + x(5,4) =e= -1;
eq6(i,j).. - y(i,j) + x(i,j) =l= 0;
eq7(i,j).. l(i,j) - w(i) + w(j) - v(i,j) + lambda(i,j) =e= 0;
eq8(i,j).. v(i,j) - R * (1 - x(i,j)) =l= 0;
eq9(i,j).. lambda(i,j) - R * (1 - (y(i,j) - x(i,j))) =l= 0;
Model contohTMB /all/;
Solve contohTMB using MIP Minimizing z;
Display "Solution values:"
Display
x.l, z.l;