Hello,
I need some help with my codes, I am new to GAMS and I don’t know how to create the constants 4 and 5, according to the PNG, for my optimization model.
In the code named “Docetaxel” (first code pasted) GAMS Studio 49 provides the right answer, but GAMS 31.1 gives a different output. My teacher wants us to use GAMS 31.1. Do you know how to fix the constrain according to the reference (Operational Constrain 5)?
In the code named “Etoposide” (second code pasted), I can not understand how to change the equation in order to provide the right answers. My output only gives pills in the meal “Breakfast”, and I want the program to find the optimal solution between the meals, without a specific sequence.
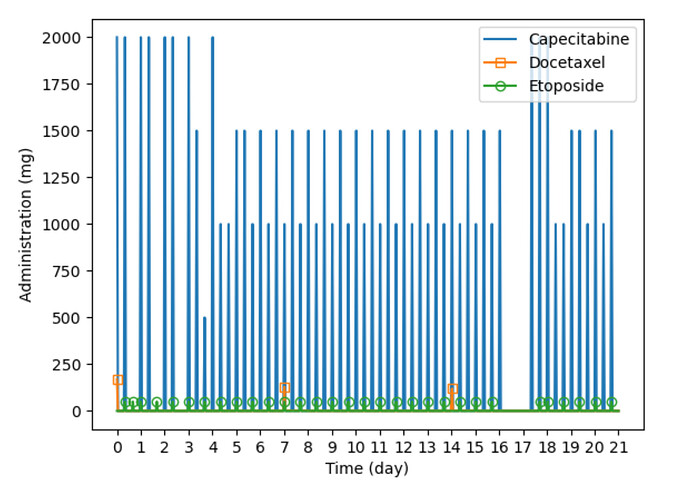
In the PNG “Results”, I provide the optimal results created by python. I want to recreate these results in GAMS 31.1. Ignore the optimal data for “Capecitabine”.
Thanks in advance!
CODE ONE:
$ TITLE Docetaxel - ChemoModel - Optimization
********** SECTION 1 **********
SET t Time Steps (21*24 hours) / 1*504 /,
m Time Steps (9 days) / day0*day20 /;
SET day(t,m) Link between hours and days;
day(t,m)$(ORD(m) = FLOOR((ORD(t)-1)/24) + 1) = YES;
ALIAS(m,mp);
********** SECTION 2 **********
SCALARS dh Time Step: 1 hour (day) / 0.041667 /,
lamda Gompertz Parameter for tumor growth rate (per day) / 7E-4 /,
V Volume of the "Effect Compartment" (m^3) / 15E-3 /,
ksi Elimination Rate of Each Drug in the body (per day) / 0.2 /,
nd Fractional Kill Efect of Each Drug in Cancer Cells (m^3\(gr*day)) / 8E-3 /,
ndw Fractional Kill Efect of Each Drug in White Cells (m^3\(gr*day)) / 8E-3 /,
rho Decrease of Drug Effectiveness (Resistance Effect) (per day) / 1.3E-2 /,
Pq_0 Initial Logarithmic Cancer Cell Population / 20.53 /,
Pmax Asymptotic Limit (Maximum Logarithmic Cancer Cell Population) / 27.53 /,
tau Delay in Toxicity (hours) = 5 days / 120 /,
a_rest Rest Period for Docetaxel (intrave-neous) (day) / 6 /,
b_eff Lower Limit for Drug Effectiveness of Each Drug (gr\m^3) / 0 /,
b_conc Maximum Permissible Concentration of Each Drug (gr) / 11.34 /,
b_cum Maximum Cumulative Daily Dose of Each Drug (gr) / 0.176 /,
b_rate Maximum Permissible Infusion rate of Each Drug (gr) / 0.176 /,
b_w Lower Bound of on WBC (cells\m^3) / 2E+12 /;
********** SECTION 3 **********
POSITIVE VARIABLES Ud(t) Administration Dose (gr),
Cd(t) Drug Concentration (gr\m^3),
Ed(t) Effective Concentration of the Drug (gr\m^3),
Cdel(t) Drug Concentration after tau (delayed)(gr\m^3);
BINARY VARIABLE Ze(t) 0:(Cd < b_eff) and 1:(Cd>=b_eff),
Zrest(m);
VARIABLES Obj Objective Function,
Pq(t) Logarithmic Cancer Cell Population;
********** SECTION 4 **********
EQUATIONS Pharmacokinetics, TumorDynamics, EffConc1, EffConc2, EffConc3, EffConc4, ConcDelay1, ConcDelay2,
MaxDose, RestDay, ObjFun;
* Pharmacokinetics and Pharmacodynamics of Cancer Cells:
Pharmacokinetics(t)$(ORD(t)>1) .. Cd(t) =E= Cd(t-1) - dh*ksi*Cd(t-1) + Ud(t-1)/V;
TumorDynamics(t)$(ORD(t)>1) .. Pq(t) =E= Pq(t-1) + dh*(lamda*(Pmax - Pq(t-1)) - nd*EXP(-rho*(ORD(t)-1)/24)*Ed(t-1));
* Linearized Effective Concentration:
EffConc1(t) .. Ed(t) =G= 0;
EffConc2(t) .. Ed(t) =G= Cd(t) - b_eff;
EffConc3(t) .. Ed(t) =L= b_conc*Ze(t);
EffConc4(t) .. Ed(t) =L= Cd(t) - b_eff + b_conc*(1-Ze(t));
* Before tau = 120 hours -> ConcDelay = 0:
ConcDelay1(t)$(ORD(t)<=tau) .. Cdel(t) =E= 1E-10;
* After tau = 120 hours -> ConcDelay = Cdel(t - tau):
ConcDelay2(t)$(ORD(t)>=tau) .. Cdel(t) =E= Cd(t - tau);
* Maximum Daily Cumulative Dose:
MaxDose(m) .. SUM(t$day(t,m), Ud(t)) =L= b_cum*(1-Zrest(m));
* Rest Period:
RestDay(m) .. SUM(mp$(ORD(mp)>=ORD(m) AND ORD(mp)<=ORD(m)+a_rest), 1 - Zrest(mp)) =L= 1;
* Minimizing the Logarithmic Cancer Cell Population at the end of treatment period
ObjFun .. Obj =E= Pq('504');
********** SECTION 5 **********
* Upper and Lower Bounds
Pq.lo(t) = 15;
Pq.up(t) = Pmax;
Cd.up(t) = b_conc;
Ud.lo(t) = 1E-15;
Ud.up(t) = b_rate;
* Initializing
Pq.fx('1') = Pq_0;
Cd.fx('1') = 1E-7;
* Proven Optimal Dose for Docetaxel:
*Ud.fx('1') = 0.17;
*Ud.fx('168') = 0.1275;
*Ud.fx('336') = 0.1275;
MODEL ask / ALL /;
OPTION MIP=CPLEX;
SOLVE ask USING MIP MINIMIZING Obj;
DISPLAY Ud.l;
CODE TWO:
$ TITLE Etoposide - ChemoModel - Optimization
********** SECTION 1 **********
SET t Time Steps (9*24 hours) / 1*216 /,
m Time Steps (9 days) / day0*day8 /,
k Meals each day / Breakfast, Lunch, Dinner /;
SET meals(t,k) Link between hours and meals / (1,25,49,73,97,121,145,169,193).Breakfast,
(9,33,57,81,105,129,153,177,201).Lunch,
(17,41,65,89,113,137,161,185,209).Dinner /;
SET NoMeal(t) No Treatment Period;
NoMeal(t)$(NOT SUM((m,k),meals(t,k))) = YES;
SET day(t,m) Link between hours and days;
day(t,m)$(ORD(m) = FLOOR((ORD(t)-1)/24) + 1) = YES;
********** SECTION 2 **********
SCALARS dh Time Step: 1 hour (day) / 0.041667 /,
lamda Gompertz Parameter for tumor growth rate (per day) / 7E-4 /,
V Volume of the "Effect Compartment" (m^3) / 15E-3 /,
ksi Elimination Rate of Each Drug in the body (per day) / 0.8 /,
nd Fractional Kill Efect of Each Drug in Cancer Cells (m^3\(gr*day)) / 5.1E-3 /,
rho Decrease of Drug Effectiveness (Resistance Effect) (per day) / 1.4E-2 /,
Pq_0 Initial Logarithmic Cancer Cell Population / 20.53 /,
Pmax Asymptotic Limit (Maximum Logarithmic Cancer Cell Population) / 27.53 /,
tau Delay in Toxicity (hours) = 5 days / 120 /,
b_eff Lower Limit for Drug Effectiveness of Each Drug (gr\m^3) / 0.5 /,
b_conc Maximum Permissible Concentration of Each Drug (gr) / 7.99 /,
b_cum Maximum Cumulative Daily Dose of Each Drug (gr) / 0.102 /,
b_rate Maximum Permissible Infusion rate of Each Drug (gr) / 0.051 /,
b_w Lower Bound of on WBC (cells\m^3) / 2E+12 /,
a_pill Pill's Mass (gr) / 0.05 /;
********** SECTION 3 **********
POSITIVE VARIABLES Ud(t) Administration Dose (gr),
Cd(t) Drug Concentration (gr\m^3),
Ed(t) Effective Concentration of the Drug (gr\m^3),
Cdel(t) Drug Concentration after tau (delayed)(gr\m^3);
BINARY VARIABLE Ze(t) 0:(Cd < b_eff) and 1:(Cd>=b_eff);
INTEGER VARIABLE Zpill(m,k) 0:Not Administered and 1:One Oral Pill etc;
VARIABLES Obj Objective Function,
Pq(t) Logarithmic Cancer Cell Population;
********** SECTION 4 **********
EQUATIONS Pharmacokinetics, TumorDynamics, EffConc1, EffConc2, EffConc3, EffConc4, ConcDelay1, ConcDelay2,
MaxDose, Pill, NoPill, ObjFun;
* Pharmacokinetics and Pharmacodynamics of Cancer Cells:
Pharmacokinetics(t)$(ORD(t)>1) .. Cd(t) =E= Cd(t-1) - dh*ksi*Cd(t-1) + Ud(t-1)/V;
TumorDynamics(t)$(ORD(t)>1) .. Pq(t) =E= Pq(t-1) + dh*(lamda*(Pmax - Pq(t-1)) - nd*EXP(-rho*(ORD(t)-1)/24)*Ed(t-1));
* Linearized Effective Concentration:
EffConc1(t) .. Ed(t) =G= 0;
EffConc2(t) .. Ed(t) =G= Cd(t) - b_eff;
EffConc3(t) .. Ed(t) =L= b_conc*Ze(t);
EffConc4(t) .. Ed(t) =L= Cd(t) - b_eff + b_conc*(1-Ze(t));
* Before tau = 120 hours -> ConcDelay = 0:
ConcDelay1(t)$(ORD(t)<=tau) .. Cdel(t) =E= 1E-7;
* After tau = 120 hours -> ConcDelay = Cdel(t - tau):
ConcDelay2(t)$(ORD(t)>=tau) .. Cdel(t) =E= Cd(t - tau);
* Maximum Daily Cumulative Dose:
MaxDose(m) .. SUM(t$day(t,m), Ud(t)) =L= b_cum;
* Pill Administration:
Pill(t,m,k)$(meals(t,k)) .. Ud(t) =E= a_pill*Zpill(m,k);
NoPill(t)$(NoMeal(t)) .. Ud(t) =E= 0;
* Minimizing the Logarithmic Cancer Cell Population at the end of treatment period
ObjFun .. Obj =E= Pq('216');
********** SECTION 5 **********
* Upper and Lower Bounds
Pq.lo(t) = 15;
Pq.up(t) = Pmax;
Cd.up(t) = b_conc;
*Ud.lo(t) = 1E-15;
Ud.up(t) = b_rate;
Zpill.up(m,k) = 4;
*Zpill.fx('day0','Dinner') = 1;
*Zpill.fx('day0','Breakfast') = 1;
* Initializing
Pq.fx('1') = Pq_0;
Cd.fx('1') = 1E-7;
Ud.fx(t)$(ORD(t)>=393 AND ORD(t)<=416) = 1E-15;
MODEL ask / ALL /;
OPTION MIP=CPLEX;
SOLVE ask USING MIP MINIMIZING Obj;
DISPLAY Ud.l;