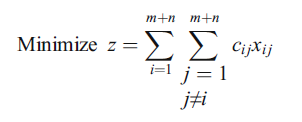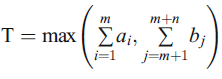Dynamic sets, set/domain assignment/violation problem

GAMS
1

I’m trying to model a transshipment problem, the mathematical formulation of which is given in the picture attached.
Transshipment model.PNG
There are m supply centers and n demand centers, and X_ij_ is the quantity shipped from center i to center j. Since in a transshipment problem, any supply or demand center can ship to any other supply or demand center, supply centers are numbers from 1 to m, whereas demand centers from m+1 to m+n.

The problem I’m facing is with writing the constraints on GAMS. After searching through some posts on the forum and going through GAMS’s YouTube tutorial on sets, I’ve been attempting to introduce dynamics sets to differentiate i, j, m and n so that these can be modeled in the constraints. I have come up with the following code for the aforementioned mathematical model.

$ title Transshipment

Set
* set of supply and demand centers
i       / Brn, Rxl, Brj, Amj, Ktm, Pkr / 
j(i)
m(i)
n(i);

j(i) = yes;

* selecting only the supply centers from i
m(i) = yes;
m('Brj') = no;
m('Amj') = no;
m('Ktm') = no;
m('Pkr') = no;

* selecting only the demand centers from i
n(i) = yes;
n('Brn') = no;
n('Rxl') = no;

Parameter
supply(i) /
Brn     40100
Rxl     46400
Brj     0
Amj     0
Ktm     0
Pkr     0 /;

Parameter
demand(j) /
Brn     0
Rxl     0
Brj     8700
Amj     35200
Ktm     20700
Pkr     5800 /;

Parameter T       86500;

Table cost(i,j)
        Brn     Rxl     Brj     Amj     Ktm     Pkr
Brn     0       243.4   250.6   280.2   511.5   490.5
Rxl     243.4   0       7.2     36.8    268.1   247.1 
Brj     250.6   7.2     0       30.4    261.7   240.7
Amj     280.2   36.8    30.4    0       231.3   210.3
Ktm     511.5   268.1   261.7   231.3   0       247
Pkr     490.5   247.1   240.7   210.3   247     0;

Positive variable
X(i,j);

Variable
Z;

Equation
obj
con1(m)
con2(n)
con3(m)
con4(n)
nnc(i,j);
obj..       sum((i,j), cost(i,j)*X(i,j)) =e= Z;
con1(m)..   sum(j, X(m,j)) =l= supply(m) + T;
con2(n)..   sum(j, X(n,j)) =e= T;
con3(m)..   sum(i, X(i,m)) =e= T;
con4(n)..   sum(i, X(i,n)) =g= demand(n) + T;
nnc(i,j)..  X(i,j) =g= 0;

Model transshipment / all /;
Options MIP = Cplex;
Solve transshipment minimizing Z using MIP;
Display X.l;

I’ve been facing the errors:
171 Domain violation for set
187 Assigned set used as domain

Where and how I did I go wrong with the way I have used sets here? Further help with modeling the constraints for different subset assignments of i and j as in the mathematical model would be much appreciated.

2

Hi
The trick is to define the assigned sets a subset. After that you have to define the variables and equation over the main set and when used referring to them by the subset.
I attached your model with these changes (and added a random value for T, but please look for a proper value).

Cheers
Renger
trans.gms (1.89 KB)

3

Hi Renger,

Thanks for the reply. I understood your approach well and knew where was I confused with assigning sets as subsets. However, the solution shows transshipment from same i to i (example: Brn to Brn). I need to model the objective function such that i is not equal to j in the second summation as shown below.
model.PNG
I tried:

j(i) = not i;

But this doesn’t seem to work and gives me error 148: “Dimension different - The symbol is referenced with more/less indices as declared”.

One more thing: Isn’t there an easy way to define T as a scalar and taking the value as defined below?
T.PNG

4

Hi
You could use a dollar constraint like this

suj(i,j)$(not sameas(i,j))

.

If a and b are parameter, you could write this as

T = max(sum(i, a(i)), sum(j$(j.val > card(m), b(j)));

Cheers
Renger

5

Pramesh,

Your formulation (the PNG file, I mean) doesn’t make sense to me. You don’t say this explicitly but T is your total shipment (i.e. total demand). How then can you have

sum_n x_{in} = T for all i in the set of supply nodes?

Your description of the problem seems inconsistent with the one in Wikipedia:

6

Oops, hit the post button.

Your description seems inconsistent with Wikipedia:

https://en.wikipedia.org/wiki/Transshipment_problem


If you define the set of all nodes as n, and partition n into supply nodes i and demand nodes j, and you have positive supply quantities sup(i) and positive demand quantities dem(j), you could have this:

b(n) is the node balance at node n: positive values indicate outflow
b(n) = sum {to, x(n,to)} + sum {from, x(from,n)} (look up ‘alias’ in the GAMS User Guide: from and to are aliases for n).
fix x(n,n) = 0 - no flow from a node to itself. Better to remove these variables from the formulation but do that in a later step.
b(i) <= sup(i) (use an explicit variable bound for this)
b(j) <= -dem(i) (again, explicit variable bound)

-Steve

7

Steve,

Yup, you’re right. The initial formulation that I was working on was the transformation of a transshipment problem to a transportation problem. Like you said, the transshipment model based on Wikipedia’s formulation is the actual linear programming model for the problem and this can be easily solved in GAMS with the use of dynamic sets as described by Renger.

  • Pramesh