Dear support team,
I am trying to write an optimization model related to the resource-constrained project schedule based on Pritsker et al. formulation. The model is as follows:
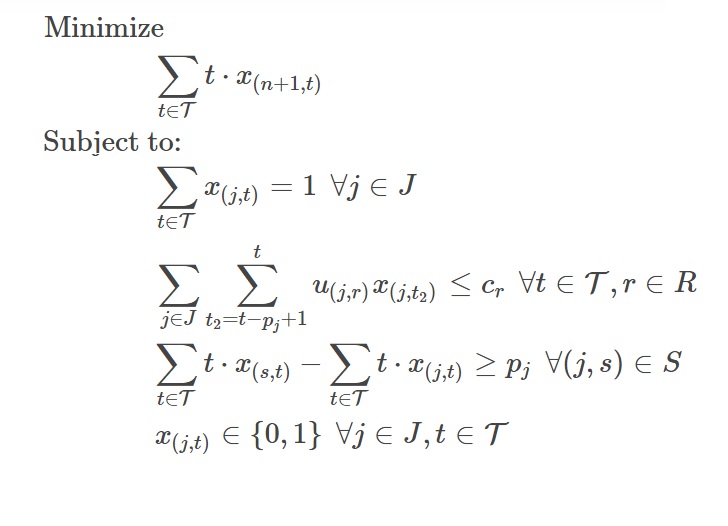
When I have defined the objective function as shown in the model, the final solution is incorrect but, when I write it in the following form, it seems to work fine.
The first attempt:
z =e= sum(t,(ord(t))*x("end",t));
The second attempt: (works fine)
z =e= sum(t,(ord(t)-1)*x("end",t));
Also, it is about the second constraint on loop for index (t2):
The first attempt:
sum((i,tt)$(ord(tt)> (max(0,(ord(t))-p(i)+1)) and ord(tt)< ord(t)+1), d(i,r)*x(i,tt)) =l= cap(r);
The second attempt: (works fine)
sum((i,tt)$(ord(tt)> (max(0,(ord(t)-1)-p(i)+1)) and ord(tt)< ord(t)+1), d(i,r)*x(i,tt)) =l= cap(r);
What I am interested to know is:
- Why we will have to define the set index (t) from (t-1)?
- In the second constraint to loop over (t2), why we will need to use (</>) in contrast to (<=/>=)? (In the second form, the solution is incorrect.).
It should be noted that in the python-based equivalent formulation, (with another solver and the same notation as the above original model), it works well without any changing in the (t) ordered.
Thanks in advance
Abbas