Hello,
I have coded the Benders decomposition for the following problem.
This is the subproblem;
And by assuming the following terminology and knowing that the subproblem does not need the feasibility cuts, the master is shown below;
And here is my code;
** benders decomposition **
*** Hybrid Car (qless) ***
** sub version: primal **
Sets
k /1*25/
r(k) /1,2,4,5,7*14,16,17,19*23/
l(k) /2*10,12*21,23*25/
n /1*1000/
onn(n)
alias(k,s,t);
Set
j(s,t)
/
$ondelim
$include qlessPairs.csv
$offdelim
/;
Set
a(s,t)
/
$ondelim
$include distance.csv
$offdelim
/;
********************************************************************************
Parameters
f(s,t)
/
$ondelim
$include qlessPairs.csv
$offdelim
/;
Parameters
d(s,t)
/
$ondelim
$include distance.csv
$offdelim
/;
Parameters
p;
p = 25;
Parameters
mu(s,t,r,n)
rho(s,t,n)
phi(s,t,n)
sigma(s,t,n);
********************************************************************************
scalar
point1, elapsed
etaUB /21000000/;
********************************************************************************
variables
master_objective, sub_objective, eta;
positive Variables
y(s,t,r)
z(s,t);
binary variable
x(k);
********************************************************************************
equation masterObj, subObj
Const1(s,t,r)
Const2(s,t)
Const3(s,t)
const4(s,t)
Const5, OptimalityCut, Consteta;
subObj..
sub_objective =e= sum((s,t)$(j(s,t)),f(s,t)*d(s,t)*z(s,t))+ sum((s,t,r)$(a(s,t)),f(s,t)*d(s,t)*y(s,t,r));
Const1(s,t,r)$(ord(s)<>ord(r) and ord(s)<>ord(t))..
y(s,t,r) =l= x.l(r);
Const2(s,t)$(ord(s)<>ord(t))..
sum(r$(ord(r)> ord(s) and ord(r)< ord(t)),y(s,t,r)) =l= 1;
Const3(s,t)$(ord(s)<>ord(t))..
z(s,t) =l= sum(l,x.l(l));
Const4(s,t)$(ord(s)<>ord(t))..
z(s,t) =l= 1;
masterObj..
master_objective =e= eta;
OptimalityCut(onn)..
eta =l= sum((s,t,r)$(ord(s)<>ord(r) and ord(s)<>ord(t)),x(r)*mu(s,t,r,onn))+sum((s,t)$(ord(s)<>ord(t)),rho(s,t,onn)+sigma(s,t,onn))
+sum((s,t,l)$(ord(s)<>ord(t)),x(l)*phi(s,t,onn));
Const5..
sum(k,x(k)) =e= p;
Consteta..
eta =l= etaUB;
option optcr = 0;
option optca = 0;
option MIP = CPLEX;
option SYSOUT = ON
option limrow = 200;
model firstMasterModel /masterObj, Const5, Consteta/
model masterModel /masterObj, Const5, OptimalityCut, Consteta/
model subModel /Const1, Const2, Const3, Const4, subObj/;
scalar
UB /inf/
LB /-inf/
iter /1/
epsilon /0.01/;
point1 = jnow;
solve FirstMasterModel using MIP maximizing master_objective;
UB = master_objective.l;
display x.l, master_objective.l;
solve subModel using LP maximizing sub_objective;
onn(n)$(n.val=iter) = yes;
mu(s,t,r,n)$(n.val=iter) = Const1.m(s,t,r);
rho(s,t,n)$(n.val=iter) = Const2.m(s,t);
phi(s,t,n)$(n.val=iter) = Const3.m(s,t);
sigma(s,t,n)$(n.val=iter) = Const4.m(s,t);
display mu, rho, phi,sigma;
iter = iter+1;
LB = eta.l+sub_objective.l;
while (LB-UB>epsilon,
solve masterModel using MIP maximizing master_objective;
UB = master_objective.l;
solve subModel using LP maximizing sub_objective;
onn(n)$(n.val=iter) = yes;
mu(s,t,r,n)$(n.val=iter) = Const1.m(s,t,r);
rho(s,t,n)$(n.val=iter) = Const2.m(s,t);
phi(s,t,n)$(n.val=iter) = Const3.m(s,t);
sigma(s,t,n)$(n.val=iter) = Const4.m(s,t);
iter = iter+1;
LB = eta.l+sub_objective.l;
display x.l, master_objective.l, mu, rho, phi,sigma;
);
elapsed=(jnow-point1)*24*3600;
display master_objective.l, UB, LB, iter, elapsed, x.l;
I know that there must be a problem with it. I want you to help me find it.
Any help is appreciated. Thank you.
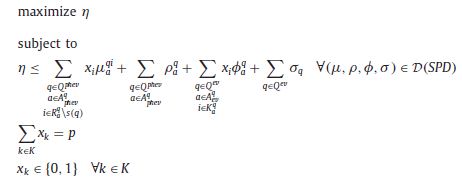
![]()

